Juegos
¡Juguemos Kenken!
Por Japheth Wood
June 2009KenKen es un puzzle nuevo inventado por Tetsuya Miyamoto, un maestro de matemáticas del Japón. KenKen significa “sabiduría al cuadrado” y se lo presenta como una variante del Sudoku. Este mes les traigo dos juegos de KenKen de 4x4. Uno más fácil con sumas solamente, y otro con más operaciones. ¡Y unas preguntas extra para los amantes de los rompecabezas matemáticos!
¿Qué es un juego KenKen?
Cada juego KenKen de 4x4 consiste en una grilla cuadrada de 4x4 dividida en grupos llamados jaulas o regiones. Las regiones vienen en diferentes tamaños: 1, 2, 3 y a veces 4 cuadrados. Cada región indica el número al que se debe llegar y una operación.
Por ejemplo, acá hay una región hecha con dos cuadrados, con un “7+” chiquito escrito en un rincón. Esto quiere decir que el número al que se debe llega es el 7 y la operación es la suma.
| 7+ |
La tarea es llenar la grilla de 4x4 usando solamente los números 1, 2, 3 y 4, de tal manera que:
- Cada número aparezca sólo una vez por fila.
- Cada número aparezca sólo una vez por columna.
- Los números en cada región, al combinarse con la operación dada, den por resultado el número al que se debe llegar.
Volviendo a nuestro ejemplo, vemos que hay exactamente dos maneras posibles de completar la región: 7 = 3 + 4 y 7 = 4 + 3 son las únicas posibilidades. La elección correcta dependerá de las primeras dos reglas, y las posibilidades para las otras regiones.
| 3 | 4 |
| 4 | 3 |
A veces una región tiene un solo cuadrado. En ese caso, el número final es dado sin ninguna operación. Esto es un regalo gratis, y es una buena manera de comenzar a completar el rompecabezas.
Esto es todo lo que necesitas para resolverlo, además de imprimir esta página para poder escribir, claro. ¡Así que a jugar KenKen!
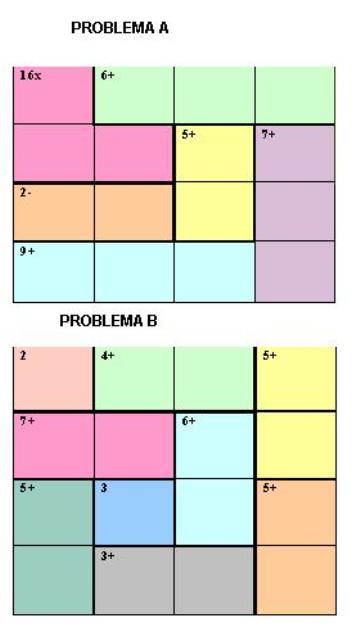
Problema A
| 16x | 6+ | ||
| 5+ | 7+ | ||
| 2- | |||
| 9+ |
Problema B
| 2 | 4+ | 5+ | |
| 7+ | 6+ | ||
| 5+ | 3 | 5+ | |
| 3+ |
El cuadrado latino
Un cuadrado de 4x4 completado con los números del 1 al 4 se llama cuadrado latino si satisface las dos condiciones de arriba. O sea, un cuadrado es latino si usa cada número sólo una vez en cada columna y en cada fila.
Problema C: ¿Cuántos diferentes cuadrados latinos puede haber si la primer fila es 4 2 1 3?
| 4 | 2 | 1 | 3 |
Puedes construir tu propio juego de KenKen empezando por el final. Primero, completa una grilla de 4x4 con un cuadrado latino. Segundo, dibuja regiones dentro de la grilla y elije una operación para cada región. Puedes empezar con la suma, para hacerlo fácil, pero los juegos de KenKen también tienen resta, multiplicación y división.
En cada región, combina los números con la operación que elegiste para determinar el número al que hay que llegar.
Ahora que tienes la solución, borra los números del cuadrado latino original, y deja los resultados y la operación de cada región. Si tu puzzle tiene una solución única, ¡tienes un juego de KenKen!
Problema D: Envíanos tu mejor puzzle de KenKen original
Si te gustó jugar al Kenken, envíanos tus soluciones a alguno de los problemas, A, B, C o D. Agradeceremos tu participación en futuros números de La Voz.
Correo:
La Voz/Bard College
PO Box 5000
Annandale-on-Hudson, NY 12504
*Japheth Wood es profesor de matemáticas en Bard College
Si quieres jugar el fabuloso KenKen, suscríbete a La Voz y recíbela cada mes por correo en tu casa.
La Voz, Cultura y noticias hispanas del Valle de Hudson
Comments | |
|
Comentario: que excelente juego m cautivo al principio no lo entendi
bien pero luego cautiva espero manden a mi correo varios de
estos gracias por su ayuda de antemano
Saludos
Fernando Posted: 3/10/2014 |
|
|
Comentario: me gustaria recibir material de
promocion y asi ver y
elegir.muchas gracia Posted: 10/30/2012 |
|
|
Comentario: no e entiendio como se juego
es mu dificil Posted: 10/25/2012 |
|
|
Comentario: Como sabes para q lado va cada
region Posted: 7/1/2011 |
|
|
Comentario: Como sabes para q lado va cada
region Posted: 7/1/2011 |
|
|
Comentario: CCC Posted: 5/28/2011 |
|
|
Comentario: HOLA:AMIGOS DE LAVOZ ES MI
PRIMERA VEZ JUGANDO KENKEN ES
TA MUY DIVERTIDO ME GUSTARIA
SABER SI LAS RESPUESTAS QUE
LES MANDE ESTAN CORRECTAS
PUES NO LE ENTENDI BIEN A LAS
INSTRUCCIONES
GRACIAS Y HASTA
PRONTO
Posted: 11/6/2009 |
|

