Juegos
El Parlamento de la Realidad
¡Una excursión matemática!
Por Japheth Wood
October 2009Con el otoño ya entre nosotros, es hora de disfrutar el tiempo fresco afuera con toda la familia. Les tengo una maravillosa sugerencia: ¡visitar una nueva escultura con mucha matemática!
El Parlamento de la Realidad (Parliament of Reality) es una escultura permanente del artista danés Olaful Eliasson que fue instalada en mayo en el campus de la universidad Bard College, justo en frente al Centro Richard B. Fisher para las Artes Escénicas (Annandale-on-Hudson, NY, 12504). La entrada es gratuita y cierra al crepúsculo.
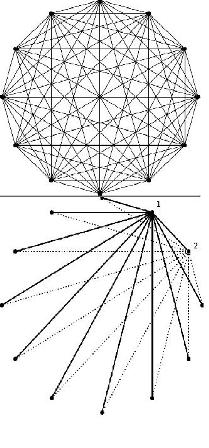
El Parlamento de la Realidad es una isleta circular de piedra que tiene 40 metros de diámetro (135 pies), rodeada por una laguna artificial y un anillo de 24 árboles. Hay doce puntos equidistantes sobre la plataforma circular, cada punto está conectado con otros once. En este diagrama se puede ver el diseño básico:
¿Cuántos segmentos de recta conectan los doce puntos de esta escultura?
A los matemáticos les encanta contar y para hacerlo han desarrollado estrategias especiales. Una manera de contar es dibujar los segmentos de una forma sistemática, como sugería el diagrama:
Empezamos conectando el punto 1 a los otros once puntos, luego el punto 2 a los otros diez puntos (ya conectamos los puntos 1 y 2 en el paso previo). Seguimos así hasta que nos damos cuenta que terminamos cuando conectamos el punto 11 con el punto 12. En total, hemos dibujado
11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 66 segmentos de recta.
Existe una manera todavía más rápida de contarlos. Cada uno de los 12 puntos está conectado con otros 11 puntos, pero si sumamos
11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 = 12 x 11, entonces contamos cada segmento de recta dos veces. Por lo tanto el número total es 6 x 11 = 66.
En perspectiva, descubrimos la sorprendente observación que
2 x (11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1) = 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11
Aquí hay otra manera de ver la misma ecuación, sumada en columnas verticales:
| 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| |
| + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
A ver si puedes adaptar esa misma estrategia para resolver estos acertijos:
Problema A: Suma estos números sin usar papel ni calculadora: 19 + 18 + 17 + … + 3 + 2 + 1
Problema B: Descubrimos que 2009 = 284 + 285 + 286 + 287 + 288 + 289 + 290
¿De cuántas maneras se puede escribir el número 2009 como la suma de (dos o más) números naturales consecutivos? Este problema es un poco más difícil así que puedes usar lápiz y papel.
Si te gustó resolver estos problemas, envíanos por favor tus soluciones o comentarios.
Correo:
La Voz / Bard College
PO Box 5000
Annandale-on-Hudson, NY 12504
[email protected]
*Japheth Wood es profesor de matemáticas en Bard College.
COPYRIGHT 2009
La Voz, Cultura y noticias hispanas del Valle de Hudson
Comments | |
| Sorry, there are no comments at this time. |

