Una torre de cubos

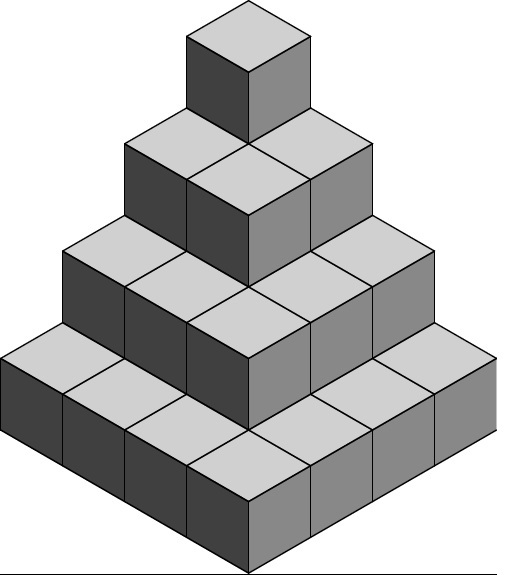
La imagen muestra una pila de cuatro capas de cubos, construida sin huecos entre sí. Intenta resolver los juegos de este mes sin tener que construir una figura con cubos de verdad.

Juego A: ¿Cuántos cubos se necesitan para construir esta figura?

Juego B: Si pintáramos el exterior de esta figura en azul (incluyendo la base), y luego separáramos los cubos, ¿cuántos cubos tendrían pintura en exactamente tres de sus caras?

Juego C: Supongamos que construimos una figura de la misma manera, pero con 100 capas de cubos. ¿Cuántos cubos se necesitarían para construirla? Después de pintarle el exterior ¿cuántos cubos tendrían pintura en exactamente tres de sus caras?

Juego D: En un juego de Kenken, cada número aparece solo una vez en cada fila y en cada columna. Los números en cada región, al combinarlos con la operación dada, dan por resultado el número que se muestra. El juego de este mes usa los números 1, 2, 4, 8 y 16 (en vez de los típicos 1, 2, 3, 4, 5).

Círculo de Matemáticas de Bard

En el Círculo de Matemáticas de Bard, los estudiantes de la escuela media disfrutan del pensamiento matemático con juegos como los presentados en esta página. El próximo encuentro en la Biblioteca de Kingston, 55 Franklin St, será el sábado 12 de abril de 1 a 3pm. ¡Gratis! ¡Ven!

Para más información visita bardmathcircle.org.

Si te gustó resolver estos problemas, envíanos por favor tus soluciones o comentarios.

Correo:

La Voz / Bard College

PO Box 5000

Annandale-on-Hudson, NY 12504

[email protected]

*Japheth Wood es profesor de matemáticas en Bard College

Soluciones: A) Se necesitan 30 cubos. B) 11 cubos. C) 338.350 cubos, de los cuales 491 están pintados en exactamente tres de sus caras.

LA VOZ, Cultura y noticias hispanas del Valle de Hudson