Cultura y noticias hispanas del Valle del Hudson
La reunión del mes pasado del Círculo de Matemáticas se centró en dos triángulos especiales: el triángulo de Pascal y el triángulo de Sierpinski. La columna de este mes es para los que se lo perdieron. ¡Vale la pena recordarlos!
COPYRIGHT 2013
La Voz, Cultura y noticias hispanas del Valle de Hudson
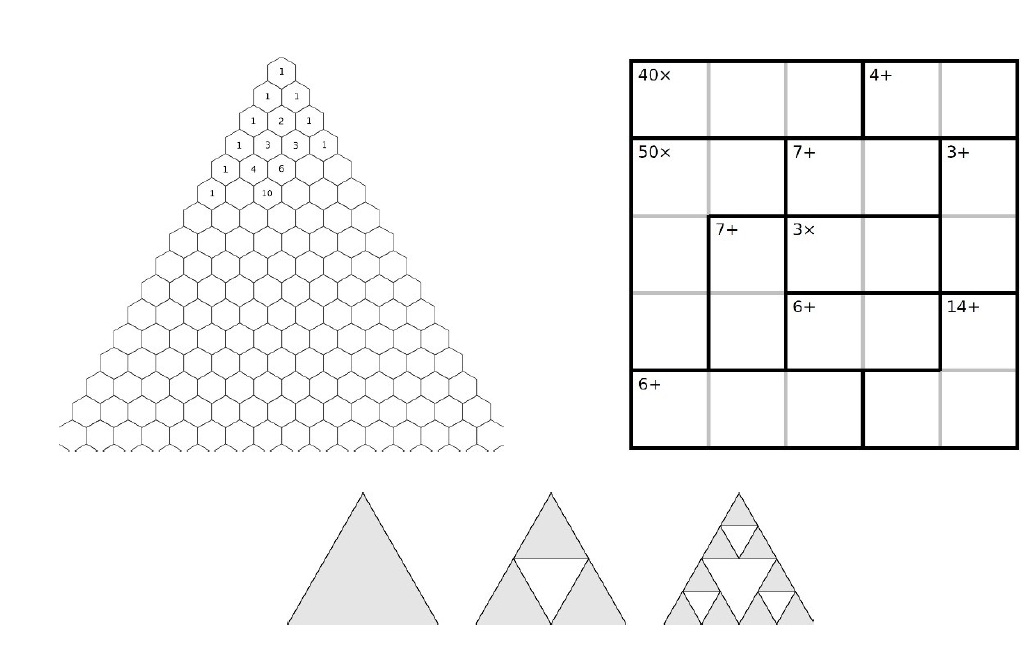
El triángulo de Pascal
Blaise Pascal (1623-1662) fue un matemático francés que desarrolló la Geometría Proyectiva y la Teoría de Probabilidad. Presentó lo que ahora se llama el triángulo de Pascal para ayudar con la computación de probabilidad. Estos números, también conocidos como coeficientes binomiales, ¡eran conocidos cientos de años antes que él!
Cada número en el triángulo de Pascal es la suma de los dos números encima suyo, y los números en los bordes izquierdos y derechos es siempre 1.
El triángulo de Sierpinski
Waclaw Sierpinski (1882-1969) fue un matemático polaco a quien se lo conoce por su trabajo en Teoría de los Conjuntos y Funciones de las Variables Reales. Desarrolló ejemplos de formas geométricas con propiedades inusuales para probar afirmaciones matemáticas en las que se creía ampliamente.
La construcción del triángulo de Sierpinski se desarrolla por etapas. Comienza con un triángulo sólido como se muestra a la izquierda. Esa es la etapa 1. Para llegar a la etapa 2 (en el medio), divide la etapa 1 en 4 triángulos y borra el triángulo del medio. Para llegar a la etapa 3 (a la derecha), divide cada uno de los triángulos que quedan de la etapa 2 en 4 triángulos y borra el triángulo central de cada uno. Luego construye la etapa 4 (que no se muestra), la etapa 5, y así sucesivamente. ¡Las etapas del triángulo de Sierpinski son infinitas!
Revista La Voz, Cultura y noticias hispanas del Valle de Hudsonback to topCOPYRIGHT 2013
La Voz, Cultura y noticias hispanas del Valle de Hudson
Comments | |
| Sorry, there are no comments at this time. |