En un número anterior de La Voz expliqué las potencias de dos: 1, 2, 4, 8, 16, 32, 64 y así sucesivamente, y mostré que cada número es la suma de dos potencias distintas de dos. Por ejemplo, 45 = 32 + 8 + 4 + 1. Esto puede ser sorprendente, pero es la idea principal del sistema numérico binario, que usan nuestras computadoras todos los días.
En la columna del mes anterior, te pregunté si es posible hacer algo similar con las potencias de tres: 1, 3, 9, 27, 81 y así sucesivamente. ¿Puedes usar una balanza de platillos y estas pesas para medir cada número entero positivo? La respuesta es otra vez un sorpresivo ¡sí! Por ejemplo, para medir 20 gramos, simplemente pon los pesos 1 y 9 en la izquierda de la balanza y 3 y 27 en la derecha. 20 gramos extra en la izquierda es precisamente el peso que equilibrará la balanza. Esto se puede ver en la fila 20 del diagrama como 9 + 1+ 20 = 3+ 27. Cada fila del diagrama muestra cómo medir un peso diferente.
Con sólo cuatro de los pesos 1, 3, 9 y 27 se puede medir cada número entero positive hasta el 40. Este es un método muy eficiente, ya que existe una manera de medir cada número entre 1 y 40.
Este mes, vamos a observar una secuencia de números muy diferente: la secuencia Fibonacci, cada número es la suma de los dos anteriores. Los dos primeros números en la secuencia son 1 y 2. Entonces 3 (= 2 + 1), 5 (= 3 + 2), 8 (= 5 + 3), 13 (= 8 + 5), y así sucesivamente. Ahora calcula el siguiente.
Juego A: Computa más números Fibonacci completando esta tabla:
| Término | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Número Fibonacci | 1 | 2 | 3 | 5 | 8 | 13 |
|
|
|
|
Ahora que tenemos muchos números Fibonacci, hagamos lo que hicimos con las potencias de dos y las potencias de tres: escribe los números enteros positivos como la suma de distintos números Fibonacci. Por ejemplo, 17 = 1 + 3 + 13. Una segunda forma es 17 = 1 + 3 + 5 + 8. En la segunda forma, los tres números 3, 5 y 8 son números Fibonacci consecutivos. Pero cuando esto ocurre, podemos remplazar los dos números Fibonacci consecutivos más altos sumándolos juntos y remplazándolos con los números Fibonacci siguientes.
Juego B: Escribe cada número hasta el 54 como la suma de números Fibonacci distintos no consecutivos. Acá tienes una tabla para comenzar:
| Número | Suma |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 1 + 3 |
| 5 | 5 |
| 6 | 1 + 5 |
| 7 | 2 + 5 |
| 8 | 8 |
| 9 | 1 + 8 |
| 10 | 2 + 8 |
| 11 | 3 + 8 |
| 12 | 1 + 3 + 8 |
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| … |
|
Juego C: Un tren directo sale de New York City a Albany a 30 millas por hora, y un tren directo sale de Albany a New York City a 20 millas por hora. ¿A qué distancia se encuentran uno del otro una hora antes de que se crucen?
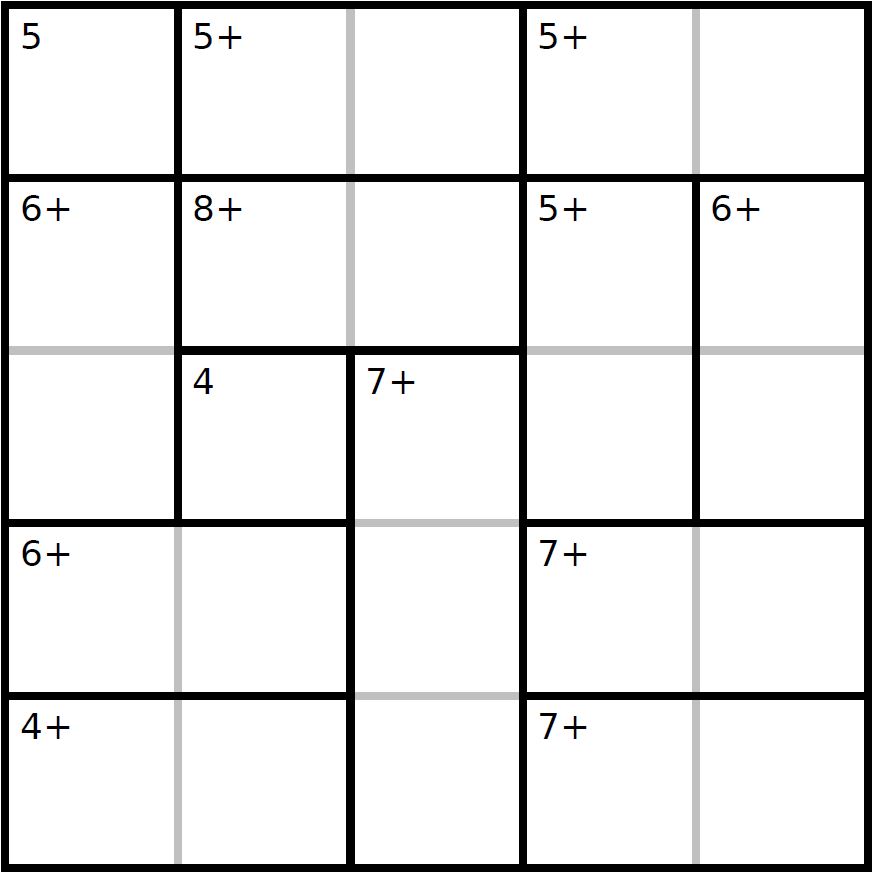
Juego D: Completa este juego de 5x5 Kenken con los números 1, 2, 3, 4 y 5. Cada número aparece solamente una vez en cada fila y en cada columna. Los números en cada región, al combinarlos según la operación dada, dan por resultado el número objetivo que se muestra.
Te esperamos en el Círculo de Matemáticas de Bard en la Biblioteca de Kingston (55 Franklin St.) para disfrutar de juegos y problemas matemáticos el sábado 8 de diciembre de 1 a 3pm.
Visita nuestro sitio Web: http://bardmathcircle.blogspot.com/
Contacta al Círculo de matemáticas por email: [email protected]
Si te gustó resolver estos problemas, envíanos por favor tus soluciones o comentarios.
Revista La Voz, Cultura y noticias hispanas del Valle de Hudson
Correo:
La Voz / Bard College
PO Box 5000
Annandale-on-Hudson, NY 12504
*Japheth Wood es profesor de matemáticas en Bard College
back to top
COPYRIGHT 2012
La Voz, Cultura y noticias hispanas del Valle de Hudson
Comments | |
| Sorry, there are no comments at this time. |