Más restas

La diferencia de los cuadrados de dos números siempre es el producto de su suma y su diferencia.

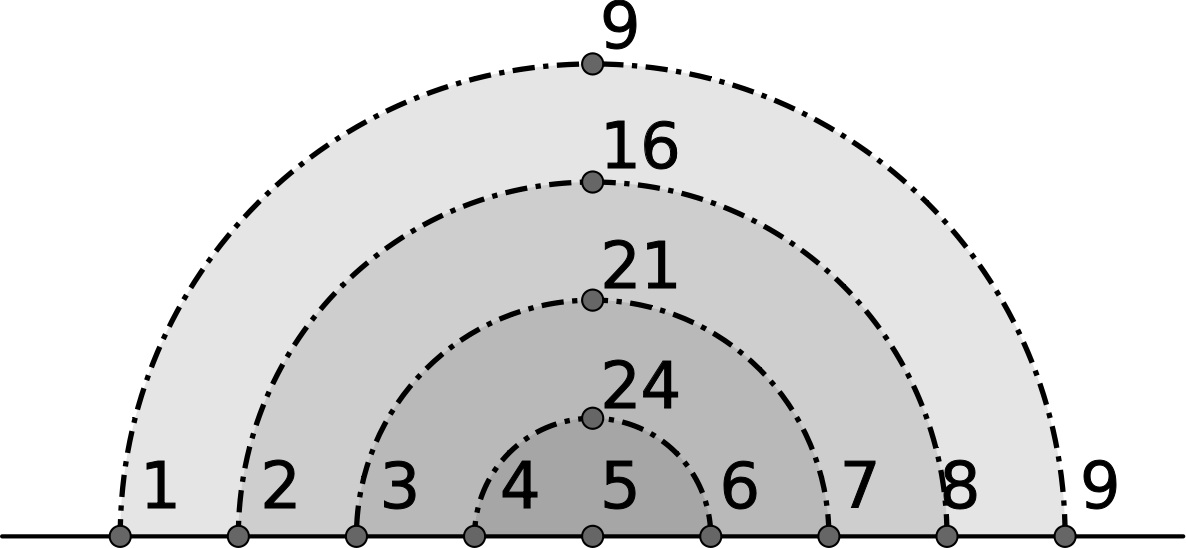
Primero, un patrón: factorizando la diferencia de dos cuadrados:

5² – 4² = 25 – 16 = 9 = 9 × 1 = (5 + 4)(5 – 4)

5² – 3² = 25 – 9 = 16 = 8 × 2 = (5 + 3)(5 – 3)

5² – 2² = 25 – 4 = 21 = 7 × 3 = (5 + 2)(5 – 2)

5² – 1² = 25 – 1 = 24 = 6 × 4 = (5 + 1)(5 – 1)

En estos cuatro ejemplos, la diferencia de los cuadrados de dos números es el producto de su suma y su resta. Con esta base ¿crees que esto es siempre verdad? Espero que no tengas 100 por ciento de confianza todavía, ya que cuatro ejemplos no son una prueba matemática.

Podemos hacer una prueba usando el poder del algebra. En vez de mirar ejemplos específicos, consideremos el proceso en general, llamando a un número a y al otro número b. Entonces la diferencia de los cuadrados de dos números es a² – b², y el producto de sus suma y resta es (a + b)(a - b). Podemos probar que estas dos cantidades es siempre la misma usando las propiedades distributivas y conmutativas de la suma y la multiplicación:

(a + b)(a - b) = (a + b) a – (a + b) b = (a² + ba) – (ab + b²) = a² + ab – ab - b² = a² - b².

Paso a paso, este proceso muestra cómo usar propiedades válidas de álgebra para probar la afirmación. Otra forma de interpretar esto es que un número es la diferencia de dos cuadrados exactamente cuando es el producto de la suma y la resta de dos números.

Apliquemos esto para expresar el número 15 como la diferencia de dos cuadrados. Ya que podemos factorizar 15 como 5 × 3, podemos suponer que 5 es la suma de dos números y 3 es la diferencia. Así:

15 = 5 × 3 = (4 + 1)(4 – 1) = 4² – 1².

¿Puedes encontrar la otra manera de expresar 15 como la diferencia de dos cuadrados?

Círculo de Matemáticas de Kingston

Muchas gracias a los que participaron del círculo de noviembre, la reunión más grande que tuvimos hasta el momento. Este año tendremos una última reunión antes de regresar en febrero, el segundo sábado de mes de 1 a 3 de la tarde en la Biblioteca de Kingston (Franklin 55): 11 de diciembre.

Por favor, envíame un correo electrónico a [email protected] para recibir información sobre los próximos eventos del Círculo de Matemáticas.

Los juegos de este mes

Juego C: Este problema es del Círculo de Matemáticas de Bard de noviembre en la Biblioteca de Kingston:

Calcula lo siguiente:

9×9+7 =

98×9+6 =

987×9+5 =

¿Hasta dónde llega este patrón?

Juego D: Encuentra todas las maneras posibles de expresar 21 como la diferencia de dos cuadrados.

 

Soluciones de noviembre:

Si te gustó resolver estos problemas, envíanos por favor tus soluciones o comentarios.

Correo:
La Voz / Bard College
PO Box 5000
Annandale-on-Hudson, NY 12504

[email protected]

*Japheth Wood es profesor de matemáticas en Bard College