Juegos
Nos seas más avaro
Por Japheth Wood
April 2013 El tema principal del mes pasado era el juego “No seas avaro”, un juego de dos jugadores con el objetivo de tomar la última o últimas monedas. Al principio del juego hay una pila de monedas de oro frente a ti y tu oponente. En cada turno tomas 1, 2 o 3 monedas (¡más sería avaro!).
El Juego A pedía recoger información: Si comienzas con diferentes números de monedas, ¿cuándo el primer jugador puede jugar y obtener un juego Ganador? Y ¿cuándo puede el segundo jugador pasar a jugar estratégicamente y ganar un juego Perdedor del primer jugador? Aquí la respuesta:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| G | G | G | P | G | G | G | P | G | G | G | P |
Parece haber un patrón para los juegos Perdedores: 4, 8, 12, … ¡todos son múltiplos de 4! Ver un patrón no necesariamente es ver la verdad, pero en este caso, sin embargo, se puede razonar. Si nuestro oponente toma 3 monedas, tomamos 1. Si toma 2, tomamos 2. Si toma 1, tomamos 3. En cada caso, en la siguiente movida de nuestro contrincante, hay 4 monedas menos en la mesa. Entonces, si nuestro oponente comienza con un múltiplo de 4, nuestro juego estratégico consiste en siempre dejarle un múltiplo de 4, así verá 8 monedas, después 4, y después perderá el juego.
El Juego B preguntaba qué pasaría si comienzas con 2013 monedas de oro. El primer jugador ganará el juego si toma 1 moneda, dejándole a su oponente 2012 monedas, que es un múltiplo de 4.
El Juego C es una variación, en la que podemos tomar exactamente 1, 4 o 7 monedas. Comenzando con 12 monedas, el primer jugador puede ganar si toma 7 monedas, dejándole 5 a su oponente. Con 5 monedas en la mesa, el contrincante puede tomar 1 moneda, dejando 4, o tomar 4 monedas, dejando 1. En cualquiera de los dos casos, el primer jugador toma las monedas restantes y gana.
Los problemas de este mes tienen que ver con una variación más complicada del juego No seas avaro, que presenté en febrero.
¡No seas más avaro!
Es igual que No seas avaro, pero en cada movida, puedes tomar cualquier número de monedas, pero no más que las que tu oponente tomó en la movida anterior (¡más sería más avaro!) y tampoco puedes tomar todas las monedas en tu primera movida (eso sería avaro).
Juego A: ¡No seas más avaro! Hay 5 monedas frente a ti y tu oponente y es tu turno. ¿Cuál es la movida estratégica que te permitirá ganar?
Juego B: ¡No seas más avaro! Si comienzas con un número impar de monedas (por lo menos 3), explica por qué siempre puedes ganar.
Juego C: ¡No seas más avaro! Comienzan con 12 monedas y es tu turno. ¿Cuál es la movida estratégica que te permitirá ganar siempre?
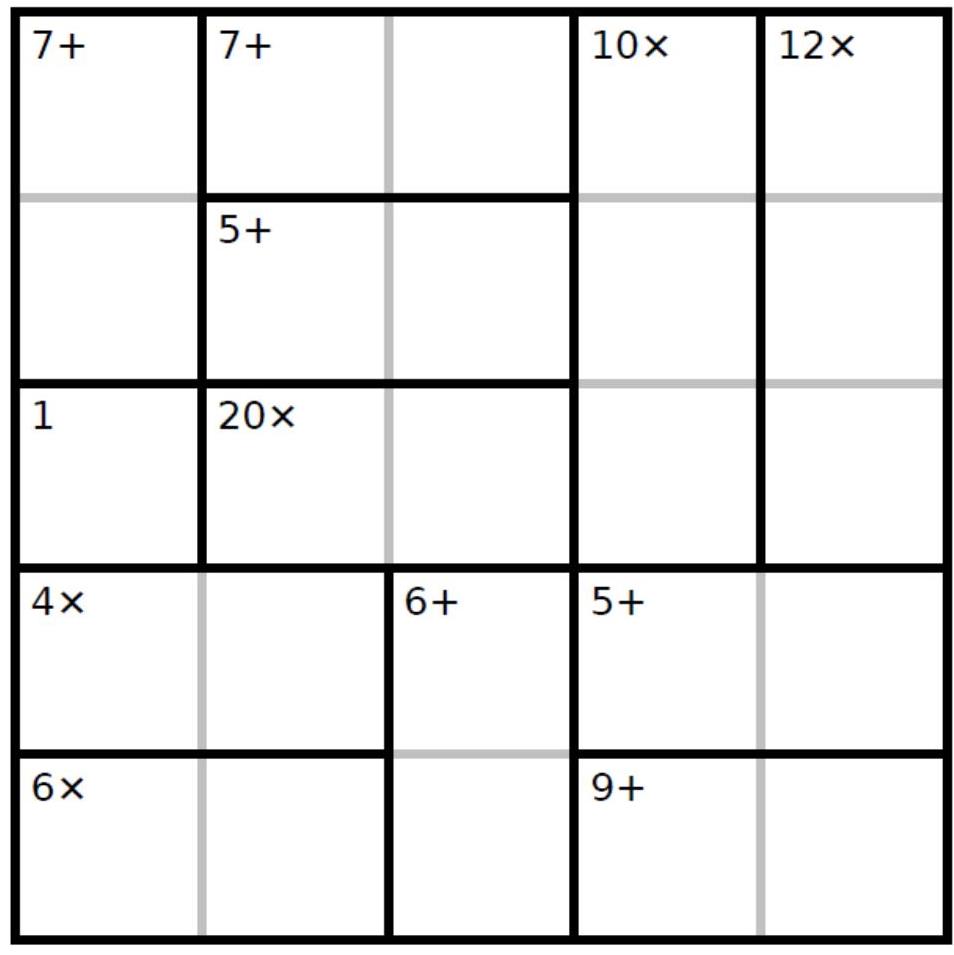
Juego D: Completa esta grilla de 5x5 de KenKen con los números 1, 2, 3, 4 y 5. Cada número aparece una sola vez en cada fila y en cada columna. Los números en cada región, al combinarlos con la operación dada, dan por resultado el número que se muestra en pequeñito.
Te esperamos en el Círculo de Matemáticas de Bard en la Biblioteca de Kingston (55 Franklin St.) para disfrutar de juegos y problemas matemáticos el sábado 13 abril de 1 a 3pm.
Visita nuestro sitio Web: http://bardmathcircle.blogspot.com/
Contacta al Círculo de matemáticas por email: [email protected]
Si te gustó resolver estos problemas, envíanos por favor tus soluciones o comentarios.
La Voz / Bard College
PO Box 5000
Annandale-on-Hudson, NY 12504
*Japheth Wood es profesor de matemáticas en Bard College
LA VOZ, Cultura y noticias hispanas del Valle de Hudson COPYRIGHT 2013
La Voz, Cultura y noticias hispanas del Valle de Hudson
Comments | |
| Sorry, there are no comments at this time. |

