¡Decimales!

La columna del mes pasado era sobre fracciones, pero muchos prefieren los decimales, así que este es el tema de este mes. Cada fracción se puede convertir en decimal usando la división larga:

Ejemplo 1: Computa el decimal de 3÷8

Después de sólo 3 pasos, el resto es 0, entonces el proceso de la división larga termina y el cociente computado es 0,375. Esto se llama un número decimal exacto.

 Ejemplo 2: Computa el decimal de 4÷11

Después de 2 pasos, el resto es 4, que es el número con el que comenzamos. Es claro que los siguientes dos pasos repetirán lo que hicimos en los primeros dos pasos, y así hasta el infinito. Esto significa que la división larga nunca terminará y el cociente es 0,36363636… con los dos dígitos “36” repitiéndose para siempre. Esto se llama un número decimal periódico. Si hay una parte que se repite en el decimal, la indicamos dibujando una línea sobre esa parte, así: 4÷11 = 0., que es mucho más corto que escribir: 0,363636363636363636363636363636363636363636363… 

Ya vimos decimales exactos y periódicos. Al usar la división larga, el decimal resultante siempre terminará o se repetirá eventualmente. Es fácil ver por qué: si en alguno de los pasos tenemos un resto de 0, el proceso de división termina y computamos un decimal exacto. Por otro lado, si en alguno de los pasos encontramos un resto que ya computamos anteriormente, el proceso comenzará a repetirse. Dado que cada resto tiene menor valor que el número por el cual estamos dividiendo, el proceso de división dará eventualmente un resto de 0, o comenzaremos a repetir.

Juego A: ¿Cuál de los siguientes se convertirán en decimales exactos?

1÷2     22÷7     11÷13     36÷125     47÷40     23÷63

Juego B: Algunas fracciones se convierten en decimales periódicos, con una parte que se repite muy larga. Por ejemplo: 3÷7 = 0,. Computa los decimales periódicos de 5÷13 y 11÷19.

Juego C: Aquí hay un número decimal que nunca se repite: 0,13113111311113111113… con bloques más y más largos del número 1 separados por el dígito 3. Este número es llamado decimal irracional. ¿Por qué este número no se puede hacer equivalente a una fracción común?

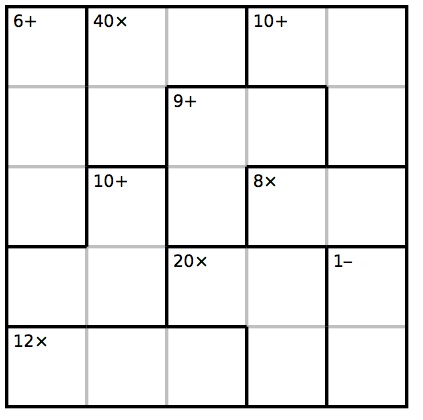
Juego D: Completa esta grilla de 5x5 de KenKen con los números 1, 2, 3, 4 y 5. Cada número aparece una sola vez en cada fila y en cada columna. Los números en cada región, al combinarlos con la operación dada, dan por resultado el número que se muestra.

Si te gustó resolver estos problemas, envíanos por favor tus soluciones o comentarios.

Correo:

La Voz / Bard College

PO Box 5000

Annandale-on-Hudson, NY 12504

[email protected]

*Japheth Wood es profesor de matemáticas en Bard College.